Restricted Boltzmann Machines with MNIST

Mar 6, 2014 0 min read

ディープ某を使った研究を再現してみたくて、最近某ニューラルネットに手を出し始めた。で、手始めにRestricted Boltzmann Machinesを実装してみたので、

  • MNISTを使って学習した結果の重み（22*22=484個）を貼っとく（↑）
  • 得た知見をまとめとく
  • Goのコード貼っとく

ってな感じで書いておく

(本当はRBMについて自分なりの解釈を書こうと思ったのだけど、それはまた今度)

実験条件

データベースはmnist。手書き数字認識で有名なアレ。学習の条件は、

  • 隠れ層のユニット数: 500
  • mini-batch size: 20
  • iterationの回数: 15

対数尤度の変化

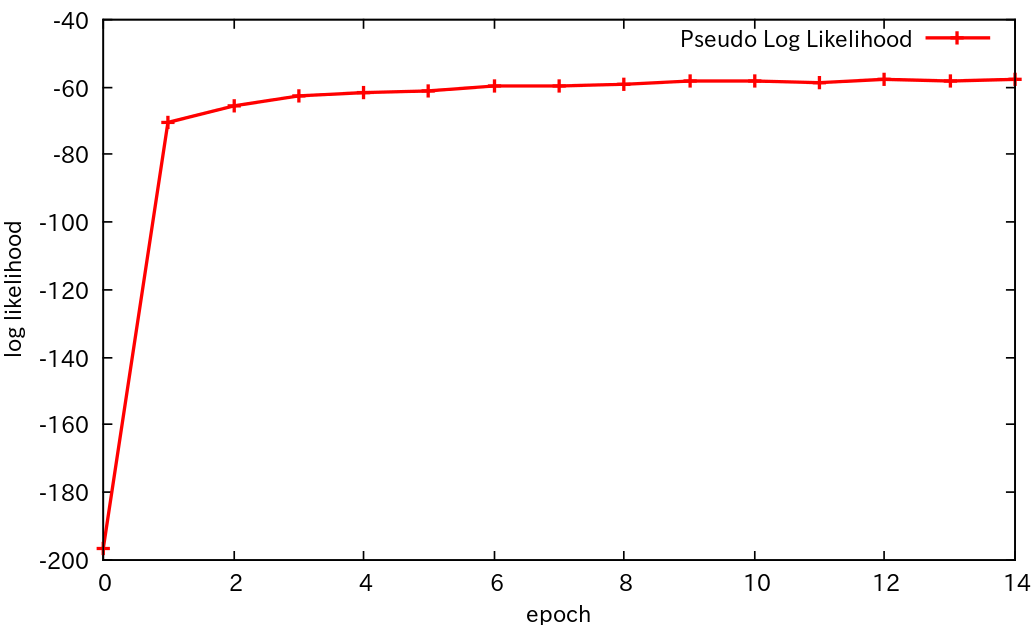
以下グラフに表示している生データ

0 -196.59046099622128
1 -70.31708616742365
2 -65.29499371647965
3 -62.37983267378022
4 -61.5359019358253
5 -60.917772257650164
6 -59.64207778426757
7 -59.42201674307857
8 -59.18497336138633
9 -58.277168243126305
10 -58.36279288392401
11 -58.57805165724595
12 -57.71043215987184
13 -58.17783142034138
14 -57.53629129936344

尤度上がると安心する。厳密に対数尤度を計算することは難しいので、Restricted Boltzmann Machines (RBM) | DeepLearning Tutorial にある擬似尤度を参考にした

学習時間

うちのcore2duoのPCで4時間弱だった気がする（うろ覚え

隠れ層のユニット数100だと、40分ほどだった

知見

今の所、試行錯誤して自分が得た知見は、

  • sample by sampleのSGDよりmini-batch SGDの方が安定して尤度上がる
  • mini-batch sizeを大きくしすぎると学習が進まない。20くらいがちょうど良かった
  • k-CD のkを大きくしてもさほど学習結果変わらない（計算コストはけっこう増すけど）
  • persistent CDを使ってもあまりよくならない（計算コストはけっこう増すけど）
  • やっぱ1-CDで十分だった
  • データの正規化方法によって結構結果も変わる。ノイズを足すかどうか、とか
  • 学習率超重要すぎわろた。今回の場合は0.1くらいかちょうど良かった
  • 隠れ層のユニット数が大きいほど学習が上手く行けばと尤度は上がる(?)

まぁだいたい A Practical Guide to Training Restricted Boltzmann Machines (PDF) に書いてあるけど、実際に肌で感じて理解した。persistent CDはもうちょっと成果出て欲しい。データ変えると成果出るんかな？

コード

コアの部分だけ、一応

package rbm

import (
	"encoding/json"
	"errors"
	"fmt"
	"github.com/r9y9/nn" // sigmoid, matrix
	"math"
	"math/rand"
	"os"
	"time"
)

// References:
// [1] G. Hinton, "A Practical Guide to Training Restricted Boltzmann Machines",
// UTML TR 2010-003.
// url: http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf
//
// [2] A. Fischer and C. Igel. "An introduction to restricted Boltzmann machines",
// Proc. of the 17th Iberoamerican Congress on Pattern Recognition (CIARP),
// Volume 7441 of LNCS, pages 14–36. Springer, 2012
// url: http://image.diku.dk/igel/paper/AItRBM-proof.pdf
//
// [3] Restricted Boltzmann Machines (RBM),  DeepLearning tutorial
// url: http://deeplearning.net/tutorial/rbm.html

// Notes about implementation:
// Notation used in this code basically follows [2].
// e.g. W for weight, B for bias of visible layer, C for bias of hidden layer.

// Graphical representation of Restricted Boltzmann Machines (RBM).
//
//     ○ ○ .... ○  h(hidden layer), c(bias)
//     /\ /\ /    /\
//    ○ ○ ○ ... ○ v(visible layer), b(bias)
type RBM struct {
	W               [][]float64 // Weight
	B               []float64   // Bias of visible layer
	C               []float64   // Bias of hidden layer
	NumHiddenUnits  int
	NumVisibleUnits int
	Option          TrainingOption
}

type TrainingOption struct {
	LearningRate        float64
	OrderOfGibbsSamping int // It is known that 1 is enough for many cases.
	Epoches             int
	MiniBatchSize       int
	L2Regularization    bool
	RegularizationRate  float64
}

// NewRBM creates new RBM instance. It requires input data and number of
// hidden units to initialize RBM.
func NewRBM(numVisibleUnits, numHiddenUnits int) *RBM {
	rbm := new(RBM)
	rand.Seed(time.Now().UnixNano())

	rbm.W = nn.MakeMatrix(numHiddenUnits, numVisibleUnits)
	rbm.B = make([]float64, numVisibleUnits)
	rbm.C = make([]float64, numHiddenUnits)
	rbm.NumVisibleUnits = numVisibleUnits
	rbm.NumHiddenUnits = numHiddenUnits

	rbm.InitRBM()
	return rbm
}

// NewRBMWithParameters returns RBM instance given RBM parameters.
// This func will be used in Deep Belief Networks.
func NewRBMWithParameters(W [][]float64, B, C []float64) (*RBM, error) {
	rbm := new(RBM)

	rbm.NumVisibleUnits = len(B)
	rbm.NumHiddenUnits = len(C)

	if len(W) != rbm.NumHiddenUnits || len(W[0]) != rbm.NumVisibleUnits {
		return nil, errors.New("Shape of weight matrix is wrong.")
	}

	rand.Seed(time.Now().UnixNano())
	rbm.W = W
	rbm.B = B
	rbm.C = C

	return rbm, nil
}

// LoadRBM loads RBM from a dump file and return its instatnce.
func LoadRBM(filename string) (*RBM, error) {
	file, err := os.Open(filename)
	if err != nil {
		return nil, err
	}
	defer file.Close()

	decoder := json.NewDecoder(file)
	rbm := &RBM{}
	err = decoder.Decode(rbm)

	if err != nil {
		return nil, err
	}

	return rbm, nil
}

// Dump writes RBM parameters to file in json format.
func (rbm *RBM) Dump(filename string) error {
	file, err := os.Create(filename)
	if err != nil {
		return err
	}
	defer file.Close()

	encoder := json.NewEncoder(file)
	err = encoder.Encode(rbm)
	if err != nil {
		return err
	}

	return nil
}

// Heuristic initialization of visible bias.
func (rbm *RBM) InitVisibleBiasUsingTrainingData(data [][]float64) {
	// Init B (bias of visible layer)
	activeRateInVisibleLayer := rbm.getActiveRateInVisibleLayer(data)
	for j := 0; j < rbm.NumVisibleUnits; j++ {
		rbm.B[j] = math.Log(activeRateInVisibleLayer[j] / (1.0 - activeRateInVisibleLayer[j]))
	}
}

func (rbm *RBM) getActiveRateInVisibleLayer(data [][]float64) []float64 {
	rate := make([]float64, rbm.NumVisibleUnits)
	for _, sample := range data {
		for j := 0; j < rbm.NumVisibleUnits; j++ {
			rate[j] += sample[j]
		}
	}
	for j := range rate {
		rate[j] /= float64(len(data))
	}
	return rate
}

// InitRBM performes a heuristic parameter initialization.
func (rbm *RBM) InitRBM() {
	// Init W
	for i := 0; i < rbm.NumHiddenUnits; i++ {
		for j := 0; j < rbm.NumVisibleUnits; j++ {
			rbm.W[i][j] = 0.01 * rand.NormFloat64()
		}
	}

	for j := 0; j < rbm.NumVisibleUnits; j++ {
		rbm.B[j] = 0.0
	}

	// Init C (bias of hidden layer)
	for i := 0; i < rbm.NumHiddenUnits; i++ {
		rbm.C[i] = 0.0
	}
}

// P_H_Given_V returns the conditinal probability of a hidden unit given a set of visible units.
func (rbm *RBM) P_H_Given_V(hiddenIndex int, v []float64) float64 {
	sum := 0.0
	for j := 0; j < rbm.NumVisibleUnits; j++ {
		sum += rbm.W[hiddenIndex][j] * v[j]
	}
	return nn.Sigmoid(sum + rbm.C[hiddenIndex])
}

// P_V_Given_H returns the conditinal probability of a visible unit given a set of hidden units.
func (rbm *RBM) P_V_Given_H(visibleIndex int, h []float64) float64 {
	sum := 0.0
	for i := 0; i < rbm.NumHiddenUnits; i++ {
		sum += rbm.W[i][visibleIndex] * h[i]
	}
	return nn.Sigmoid(sum + rbm.B[visibleIndex])
}

// GibbsSampling performs k-Gibbs sampling algorithm,
// where k is the number of iterations in gibbs sampling.
func (rbm *RBM) GibbsSampling(v []float64, k int) []float64 {
	// Initial value is set to input
	vUsedInSamping := make([]float64, len(v))
	copy(vUsedInSamping, v)

	for t := 0; t < k; t++ {
		sampledH := make([]float64, rbm.NumHiddenUnits)
		for i := 0; i < rbm.NumHiddenUnits; i++ {
			p := rbm.P_H_Given_V(i, vUsedInSamping)
			if p > rand.Float64() {
				sampledH[i] = 1.0
			} else {
				sampledH[i] = 0.0
			}
		}
		for j := 0; j < rbm.NumVisibleUnits; j++ {
			p := rbm.P_V_Given_H(j, sampledH)
			if p > rand.Float64() {
				vUsedInSamping[j] = 1.0
			} else {
				vUsedInSamping[j] = 0.0
			}
		}
	}

	return vUsedInSamping
}

func flip(x []float64, bit int) []float64 {
	y := make([]float64, len(x))
	copy(y, x)
	y[bit] = 1.0 - x[bit]
	return y
}

// FreeEnergy returns F(v), the free energy of RBM given a visible vector v.
// refs: eq. (25) in [1].
func (rbm *RBM) FreeEnergy(v []float64) float64 {
	energy := 0.0

	for j := 0; j < rbm.NumVisibleUnits; j++ {
		energy -= rbm.B[j] * v[j]
	}

	for i := 0; i < rbm.NumHiddenUnits; i++ {
		sum := rbm.C[i]
		for j := 0; j < rbm.NumVisibleUnits; j++ {
			sum += rbm.W[i][j] * v[j]
		}
		energy -= math.Log(1 + math.Exp(sum))
	}

	return energy
}

// PseudoLogLikelihood returns pseudo log-likelihood for a given input data.
func (rbm *RBM) PseudoLogLikelihood(v []float64) float64 {
	bitIndex := rand.Int() % len(v)
	fe := rbm.FreeEnergy(v)
	feFlip := rbm.FreeEnergy(flip(v, bitIndex))
	cost := float64(rbm.NumVisibleUnits) * math.Log(nn.Sigmoid(feFlip-fe))
	return cost
}

// PseudoLogLikelihood returns pseudo log-likelihood for a given dataset (or mini-batch).
func (rbm *RBM) PseudoLogLikelihoodForAllData(data [][]float64) float64 {
	sum := 0.0
	for i := range data {
		sum += rbm.PseudoLogLikelihood(data[i])
	}
	cost := sum / float64(len(data))
	return cost
}

// ComputeGradient returns gradients of RBM parameters for a given (mini-batch) dataset.
func (rbm *RBM) ComputeGradient(data [][]float64) ([][]float64, []float64, []float64) {
	gradW := nn.MakeMatrix(rbm.NumHiddenUnits, rbm.NumVisibleUnits)
	gradB := make([]float64, rbm.NumVisibleUnits)
	gradC := make([]float64, rbm.NumHiddenUnits)

	for _, v := range data {
		// Gibbs Sampling
		gibbsStart := v
		vAfterSamping := rbm.GibbsSampling(gibbsStart, rbm.Option.OrderOfGibbsSamping)

		// pre-computation that is used in gradient computation
		p_h_given_v1 := make([]float64, rbm.NumHiddenUnits)
		p_h_given_v2 := make([]float64, rbm.NumHiddenUnits)
		for i := 0; i < rbm.NumHiddenUnits; i++ {
			p_h_given_v1[i] = rbm.P_H_Given_V(i, v)
			p_h_given_v2[i] = rbm.P_H_Given_V(i, vAfterSamping)
		}

		// Gompute gradient of W
		for i := 0; i < rbm.NumHiddenUnits; i++ {
			for j := 0; j < rbm.NumVisibleUnits; j++ {
				gradW[i][j] += p_h_given_v1[i]*v[j] - p_h_given_v2[i]*vAfterSamping[j]
			}
		}

		// Gompute gradient of B
		for j := 0; j < rbm.NumVisibleUnits; j++ {
			gradB[j] += v[j] - vAfterSamping[j]
		}

		// Gompute gradient of C
		for i := 0; i < rbm.NumHiddenUnits; i++ {
			gradC[i] += p_h_given_v1[i] - p_h_given_v2[i]
		}
	}

	return gradW, gradB, gradC
}

func (rbm *RBM) ParseTrainingOption(option TrainingOption) error {
	rbm.Option = option

	if rbm.Option.MiniBatchSize <= 0 {
		return errors.New("Number of mini-batchs must be larger than zero.")
	}
	if rbm.Option.Epoches <= 0 {
		return errors.New("Epoches must be larger than zero.")
	}
	if rbm.Option.OrderOfGibbsSamping <= 0 {
		return errors.New("Order of Gibbs sampling must be larger than zero.")
	}
	if rbm.Option.LearningRate == 0 {
		return errors.New("Learning rate must be specified to train RBMs.")
	}

	return nil
}

// Train performs Contrastive divergense learning algorithm to train RBM.
// The alrogithm is basedd on (mini-batch) Stochastic Gradient Ascent.
func (rbm *RBM) Train(data [][]float64, option TrainingOption) error {
	err := rbm.ParseTrainingOption(option)
	if err != nil {
		return err
	}

	numMiniBatches := len(data) / rbm.Option.MiniBatchSize

	for epoch := 0; epoch < option.Epoches; epoch++ {
		// Monitoring
		fmt.Println(epoch, rbm.PseudoLogLikelihoodForAllData(data))

		for m := 0; m < numMiniBatches; m++ {
			// Compute Gradient
			batch := data[m*rbm.Option.MiniBatchSize : (m+1)*rbm.Option.MiniBatchSize]
			gradW, gradB, gradC := rbm.ComputeGradient(batch)

			// Update W
			for i := 0; i < rbm.NumHiddenUnits; i++ {
				for j := 0; j < rbm.NumVisibleUnits; j++ {
					rbm.W[i][j] += rbm.Option.LearningRate * gradW[i][j] / float64(rbm.Option.MiniBatchSize)
					if rbm.Option.L2Regularization {
						rbm.W[i][j] *= (1.0 - rbm.Option.RegularizationRate)
					}
				}
			}

			// Update B
			for j := 0; j < rbm.NumVisibleUnits; j++ {
				rbm.B[j] += rbm.Option.LearningRate * gradB[j] / float64(rbm.Option.MiniBatchSize)
			}

			// Update C
			for i := 0; i < rbm.NumHiddenUnits; i++ {
				rbm.C[i] += rbm.Option.LearningRate * gradC[i] / float64(rbm.Option.MiniBatchSize)
			}
		}
	}

	return nil
}

使い方とかは察して（どうせ誰も使わないはず

今は、通常のRBMのvisible layerを連続値に拡張した Gaussian Bernoulli RBMを学習しようとしてるんだけど、これがムズイ。実装ミスもあるかもだけど、局所解に落ちまくってる気がする。

Gaussian Bernoulli RBM、Deep Belief Networks, Deep Neural Networksについてはまた今度

2014/05/11 要望があったので、もろもろコードあげました https://github.com/r9y9/nnet

参考資料

Deep Learning RBM Machine Learning
Ryuichi Yamamoto
Ryuichi Yamamoto
Engineer/Researcher

I am a engineer/researcher passionate about speech synthesis. I love to write code and enjoy open-source collaboration on GitHub. Please feel free to reach out on Twitter and GitHub.

Related