逆連続ウェーブレット変換による信号の再構成

やったのでメモ。おそらく正しくできたと思う。結果貼っとく。ウェーブレットの参考は以下の文献

Torrence, C. and G.P. Compo “A Practical Guide to Wavelet Analysis”, Bull. Am. Meteorol. Soc., 79, 61–78, 1998.

ウェーブレットの条件

マザーウェーブレットはmorletを使う

文献に従って$\omega_{0} = 6.0$とした。

以下にいっぱい図を張る。軸は適当

元の信号

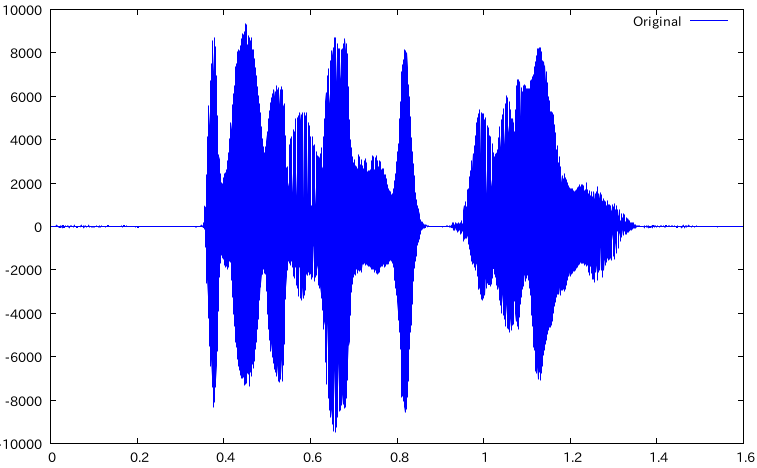
ウェーブレットスペクトログラム

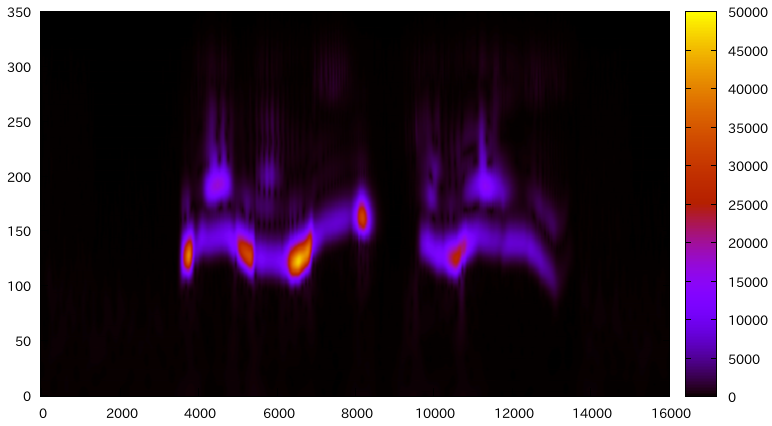
Gaborではなく、Morletで求めたもの。スケールは、min=55hzで、25cent毎に8オクターブ分取った。一サンプル毎にウェーブレット変換を求めてるので、前回の記事でガボールウェーブレットで求めた奴よりよっぽど解像度高いっすね（前のは10ms毎だった、書いてなかったけど）。見てて綺麗（こなみ

計算はFFT使ってるので速い

http://hp.vector.co.jp/authors/VA046927/gabor_wavelet/gabor_wavelet.html スケールのとり方はここを参考にするといい

再構成した信号

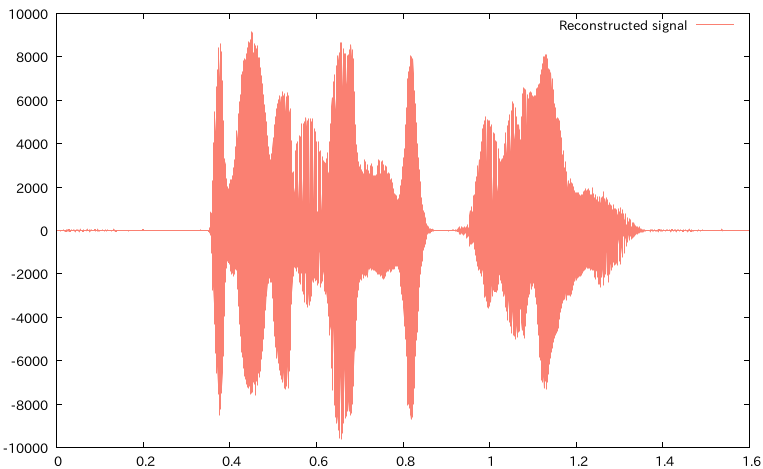
連続ウェーブレットの逆変換は、フーリエ変換と違ってそんなシンプルじゃないんだけど、結果から言えばウェーブレット変換の実数部を足しあわせて適当にスケールすれば元の信号が再構成できるみたい。ほんまかと思って実際にやってみたけど、できた

が、実は少し誤差がある

重ねてプロット

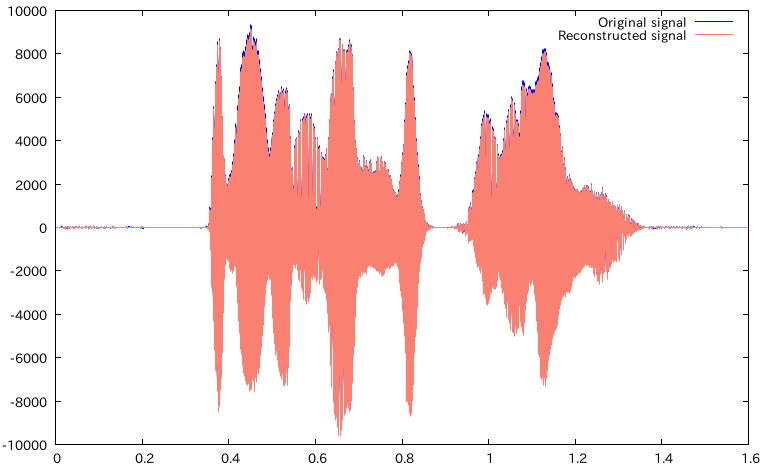
あっぷ

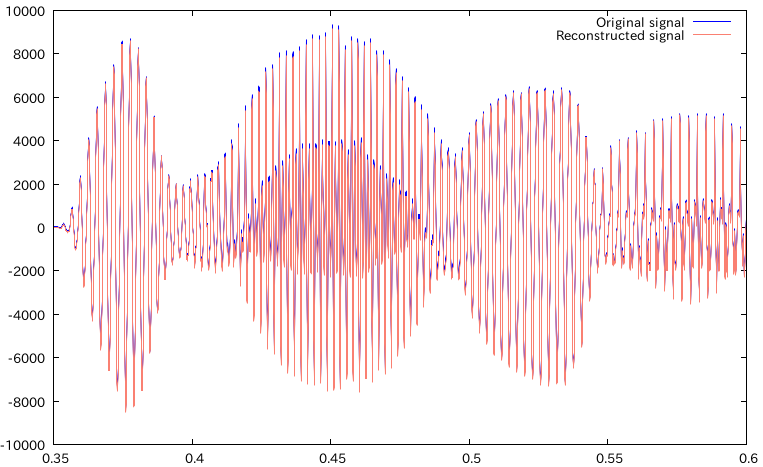
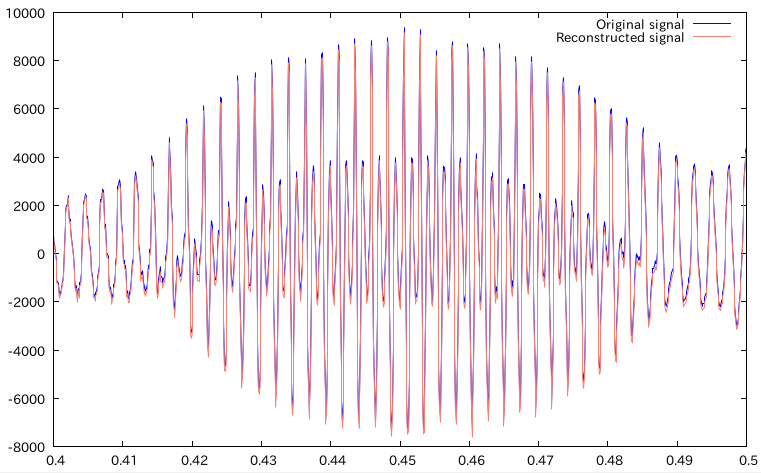
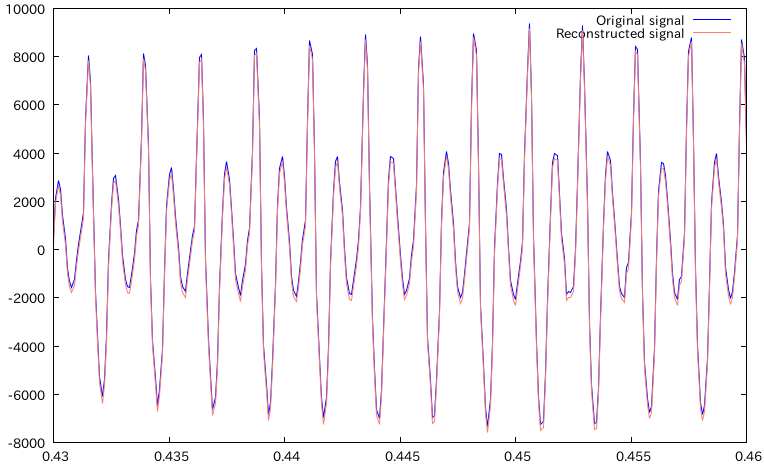
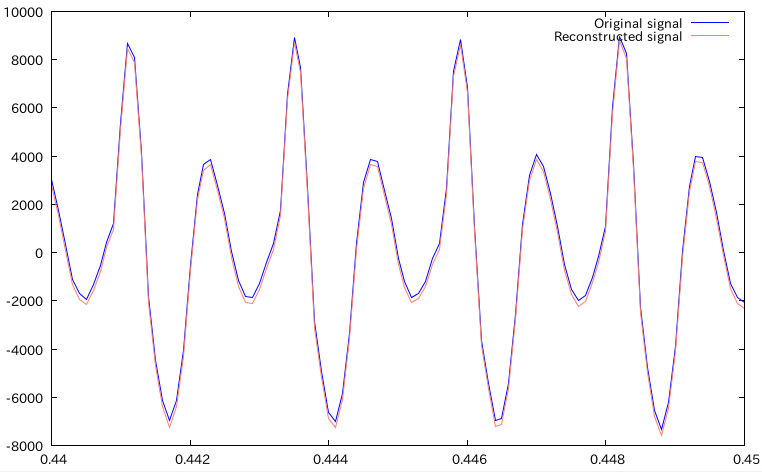
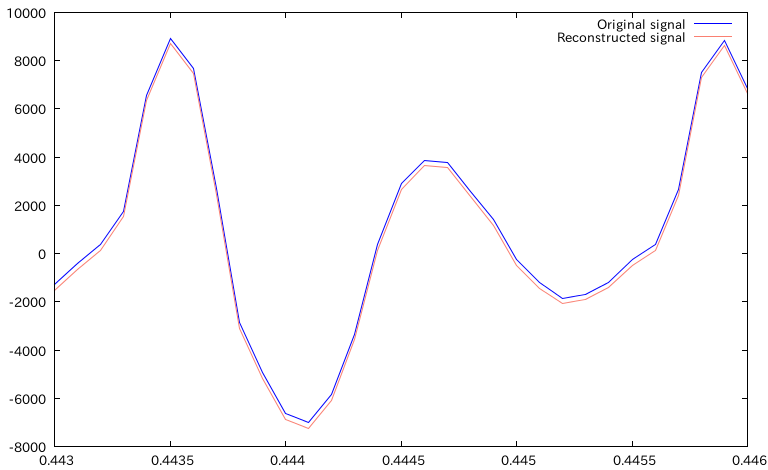
んー、まぁだいたいあってんじゃないですかね

誤差

平均誤差を計算すると、図の縦軸の量で考えて55.3994だった。16bitのwavが-32768〜32767なので、どうだろう、大きいのか小さいのかわからん

ただ、再合成した音声を聞いた所それほど違和感はなかった。これはつまり、スペクトルいじる系の分析にSTFTがではなくウェーブレット使ってもいいんではないか？という考えが生まれますね。果たして、ウェーブレットが音声/音楽の分析にフーリエ変換ほど使われないのはなぜなのか、突き詰めたい

メモ

http://paos.colorado.edu/research/wavelets/wavelet3.html ここの最後に書かれている以下の文章、

One problem with performing the wavelet transform in Fourier space is that this assumes the time series is periodic. The result is that signals in the wavelet transform at one end of the time series will get wrapped around to the other end.

FFT使うウェーブレット変換の問題は、信号を周期関数として仮定してしまうことにある、と。まあ、ですよねー。信号がめちゃくちゃ長くてこの仮定が破綻してしまう場合、どうするのがいいんだろう。

あと、FFT使うウェーブレットの問題として、メモリ食うってのがあるんよな。ウェーブレット変換を計算する前に、マザーウェーブレットのフーリエ変換を持っとかないといけないし、サンプル毎に計算しないといけないし。44.1kの数分の音声とかなると、もう無理っすね。

それぞれ、解決方法は思いつかないでもないけど、まだまとまってないので、解決したらまとめる、かもしれない。

さらにめも

• practicalなんちゃらの、マザーウェーブレットを正規化する部分のmatlabコード、文献中の数式と若干違ってトリッキー。展開すれば一緒なんだけど、文献中の数式をそのまま書いたようになってないので、注意。ちょっと戸惑った
• 逆ウェーブレットを行う際のスケールにかかる係数（文献中でいう$C_{\delta}$）は、マザーウェーブレットが決まれば値が定まる（らしい）。例えばMorletの$\omega_0 = 6$なら0.776とわかってるので、積分して計算する必要はない
• ウェーブレット変換と戯れてたら週末終わった