連続ウェーブレット変換に使うマザーウェーブレット色々: Morlet, Paul, DOG

「ウェーブレット変換って難しいんじゃ…マザーウェーブレット？よくわかんない…」

大丈夫、そんな人には以下の文献がお勧めです

Torrence, C. and G.P. Compo “A Practical Guide to Wavelet Analysis”, Bull. Am. Meteorol. Soc., 79, 61–78, 1998.

前置きはさておき、上の文献を参考にMorlet, Paul, DOG (Derivative of Gaussian) の代表的な3つのマザーウェーブレットで音声に対してウェーブレット変換をしてみたので、メモがてら結果を貼っておく

図の横軸はサンプルで、縦軸は周波数Hz（対数目盛り）にした

マザーウェーブレットのパラメータは、Morletは $\omega_{0} = 6.0$、Paulは $M = 4$、DOGは $M = 6$

スケールは、min=55hzで、25cent毎に8オクターブ分取った※厳密には違うのでごめんなさい

分析に使った音声は、逆連続ウェーブレット変換による信号の再構成 - LESS IS MORE で使ったのと同じ

Morlet

Paul

DOG

対数を取ると、以下のような感じ

Morlet

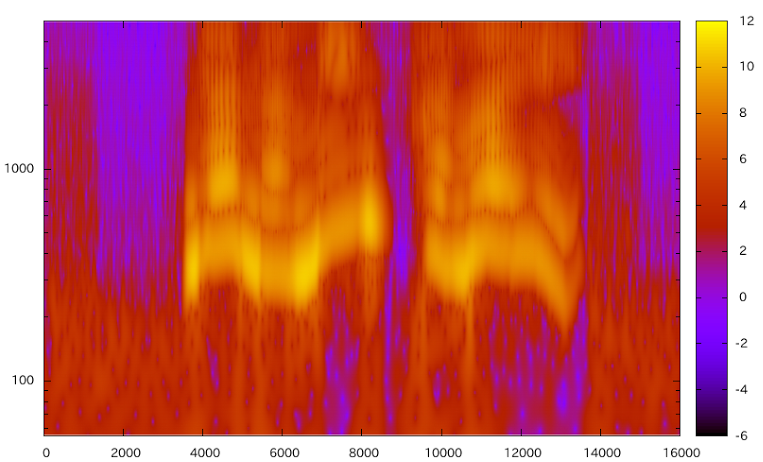
Paul

DOG

Paulは時間解像度は高いけど周波数解像度はいまいちなので、音声とかには向かないのかなー。DOGはMorletとPaulの中間くらいの位置づけの様子。DOGはorderを上げればMorletっぽくなるけど、Morletの方がやっぱ使いやすいなーという印象。

スケールから周波数への変換

実は今日まで知らなかったんだけど、マザーウェーブレットによっては時間領域でのスケールの逆数は必ずしも周波数領域での周波数に対応するとは限らないそう。というかずれる（詳細はPractical Guideの3.hを参照）。上で書いた厳密には違うというのは、これが理由。

ただし、スケールから周波数への変換はマザーウェーブレットから一意に決まるようなので、正しい周波数を求めることは可能。上に貼った図は、Practical Guideにしたがってスケールから周波数に変換している。

例えば、$f = \frac{1}{s}$となるようにスケールを与えていたとき、$\omega_0 = 6.0$のMorletを使ったウェーブレット変換の真の周波数は、

となる。 $\omega_0 = 6.0$のMorletだとスケールの逆数にほぼ一致するので今まで気づかなかった…

めんどくさい。これを知ってからちょっとウェーブレット嫌いになった。でもめげない

おわり

参考

• Torrence, C. and G.P. Compo “A Practical Guide to Wavelet Analysis”, Bull. Am. Meteorol. Soc., 79, 61–78, 1998.
• Continuous Wavelet Transform Reconstruction Factors for Selected Wavelets
• HULINKS | テクニカルサポート | FlexPro | 連続ウェーブレット変換 (CWT)

前書いた記事

• FFTを使った連続ウェーブレット変換の高速化 - LESS IS MORE
• 逆連続ウェーブレット変換による信号の再構成 - LESS IS MORE